Overview of Basic Graph Traversal Algorithm

"Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). Graphs are one of the principal objects of study in discrete mathematics." ... from Wiki page.

Brief

Recently, I explored the basic implementation of graphs, BFS/DFS search, shortest path problem, and discovered its algorithm. It should be grateful that I have learned the fundamentals of mathematics and programming in college, so that I could learn and get a basic understanding of how the graph traversal algorithm work, and further make the computer do it. In this post, I would like to discuss the basic concepts, practice the simple implementation of BFS and DFS with the directed graph and undirected graph.

Graph Search Algorithm

In computer science, a graph is an abstract data type that is meant to implement the undirected grpah and directed graph concept from the field of a graph theory. A graph data structure consists of a finite set of vertices, together with a set of unordered or ordered paired of these vertices. The graph search (also known as graph traversal) algorithm uses a recursion and linked list based stack to determine a route from a single point on a graph to another single point on a graph. In addition to the structure, there are two basic types of graph search: breadth-first search (BFS) and depth-first search (DFS). The major difference between those type is that the data structure requires a queue (BFS) or stack (DFS).

Directed Graph

I recapped and practiced the simple C++ BFS/DFS implementation with directed graph initially inspired by Practice Directed Graph then reworked.

Ordered paired, Unweight and Directed Graph Database

The basic functions for the directed graph implementation are as follows:

• BFS (Breadth-first search): use queue and traversal all the connected nodes
• DFS (Depth-first search): use stack and traversal all the connected nodes
• Detect Cycle in a Directed Graph: check whether the graph contains a cycle or not
• Iterate in a Directed Graph: pointing to all of vertices in the directed graph

Here is the python/cpp interface of directed graph traversing:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def main():
    dg = DirectedGraph()
    dg.add_edge(0, 1)
    dg.add_edge(0, 5)
    dg.add_edge(1, 2)
    dg.add_edge(2, 4)
    dg.add_edge(2, 6)
    dg.add_edge(3, 2)
    dg.add_edge(5, 8)
    dg.add_edge(6, 5)
    dg.add_edge(7, 5)
    p1 = dg.bfs()

if __name__ == '__main__':
    main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

int main(int argc, char *argv[])
{
    auto graph_node = new GraphDirected(GraphRepresentation::kRepresentationTypeList);
    graph_node->AddEdge(0, 1);
    graph_node->AddEdge(0, 5);
    graph_node->AddEdge(1, 2);
    graph_node->AddEdge(2, 4);
    graph_node->AddEdge(2, 6);
    graph_node->AddEdge(3, 2);
    graph_node->AddEdge(5, 8);
    graph_node->AddEdge(6, 5);
    graph_node->AddEdge(7, 5);
    graph_node->DFS();
    graph_node->BFS();
}

Breadth-first Search (BFS)

Breadth-first search is traversing algorithm where you should start traversing from a selected node (source or parnet node) and traverse the graph layerwise thus exploring the neighbor nodes. In other words, it starts at the tree root and explors all nodes at the present depth prior to moving on to the nodes at the next depth level. In addition to the traverse, BFS might be the easiest one to understand because the only data structure it requires is a queue.

Depth-first Search (DFS)

Depth-first search is recursive algorithm that uses the idea of backtracking. It involves searches of all the nodes by going ahead if possible, else by backtracking. In order words, it starts at the root (select in some arbitrary node) and explores as far as possbile along each branch before backtracking.

Undirected Graph

I also recapped and practiced the basic BFS/DFS implemenation with undirected graph matrix initially inspired by Practice Undirected Graph Matrix then reworked.

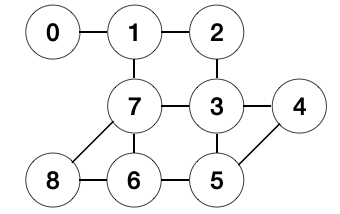Ordered paired, Unweight and Undirected Graph Database

The basic functions for the understand graph are as follows:

• BFS (Breadth-first search): use queue and recrusively traversal all the connected nodes
• DFS (Depth-first search): use stack and recrusively traversal all the connected nodes

Here is the python interface of graph traversing:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def main():
    udg = UndirectedGraph()
    udg.add_edge(0, 1)
    udg.add_edge(1, 2)
    udg.add_edge(2, 3)
    udg.add_edge(1, 7)
    udg.add_edge(3, 7)
    udg.add_edge(7, 8)
    udg.add_edge(3, 4)
    udg.add_edge(3, 5)
    udg.add_edge(4, 5)
    udg.add_edge(5, 6)
    udg.add_edge(6, 7)
    udg.add_edge(6, 8)

if __name__ == '__main__':
    main()

Shortest Path Problem

In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of it consitiuent edges is minimized.

The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weights by the length of the segments.

The most important algorithms for solving this problem are: + Dijkstra's algorithm: solves the single-source shortest path problem with non-negative edge weight. + Bellman-Ford algorithm: solves the single-source problem if edge weight may be negative.

Here, I only come up through the Dijkstra's algorithm with undirected graph initially, which inspired by then learned how it implements.

The basic functions for the undirected graph are as follows:

• Add edges in the graph and iterally get vertex: pointing out all of vertices in the undirected graph
• Dijkstra's algorithm: use priority queue and traversal all the connected nodes

Dijkstra's Algorithm

Dijkstra's algorithm initially starts with infinite distances and then try to improve them step to find the shortest path from a single source to the closest of a set of target nodes on finite graph. Continue this process of updating the neighbor intersections with the shortest distance, making the current intersection as visited, and moving onto a closet unvisited intersection until you have marked the destination as visited.

Conclusions

Graph databases are efficient with respects to local data analysis. We should always be aware of that many search and traversal applications in practice are implemented using modified breadth-first and depth-first search algorithm.

Reference

• Wiki: Graph theory

• Wiki: Breadth-first search

• Wiki: Depth-first search

Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)